Simulating the Rate of Profit
The tendency for the rate of profit to fall is a famous theory advanced by the classical political economists, particularly Marx. He believed that this tendency was the result of an ever increasing level of fixed capital, the result of capitalist competition and the necessity to expand production. The rate of profit equation is S/(C+V), where S stands for Surplus (profit), C stands for constant capital (machinery and non-labor inputs), and V stands for variable capital (labor inputs). Therefore, in Marx’s formulation, the rate of profit would tend to fall in the long term, despite temporary counter-tendencies, due to an ever increasing magnitude of C relative to S and V.
In order to better understand these dynamics, I created a simulation which shows how the rate of profit changes given the different ways that capitalism reproduces itself.
In order to simplify the math involved, rather than dealing with the absolute magnitudes of labor hours and capital stock, the models deals with each variable as a share of total output - it is a zero sum game. This assumption is based on the fact that at any given moment there is a fixed amount of labor, both living and dead, being utilized in production, and the effects of the previous production cycle’s change to the capital stock will determine the proportions of this cycle’s 3 variables, S, C, and V.
The model begins with an arbitrary starting proportions - if we liked we could use real world data - and is then transformed according to a series of functions. These arbitrary values are added up to a sum, and as mentioned before, this sum (total in the equations below) will not change throughout the transformation, except due to rounding.
The first calculation is the most simple, the current level of constant capital calculated as “depreciation” (which here would include all non-labor inputs used up in production, not just wear and tear on machinery).
C = Capital Stock / Average Depreciation Time
C, then, is the proportion of dead labor in the economy. Those commodities which are the product of previous labor, and which are being used up over time in production. In particular, it is that amount which is being used up which is expressed in the value created in an economy, in C. By knowing how much of the labor is dead labor, we can now see how living labor is being apportioned in the economy.
S = (total - C) * Rate of Exploitation
The rate of exploitation is one of the three independent variables in this model, which we can vary to see how it affects the system overall. The equation for this ratio is slightly different than Marx’s - rather than S/V, it’s S/(V+S) This ratio determines how much income goes towards capital vs labor.
V = (total - C) * (1 - Rate of Exploitation)
To get labor’s share, V, all we have to do is invert the rate of exploitation.
Since V will be used for subsistence goods, the last independent variable we must deal with is the rate of capitalist consumption. The equation for the Rate of Capitalist Consumption is Consumption/(Consumption + Investment).
Capitalist Consumption = S * Rate of Capitalist Consumption
What surplus hasn’t been used for capitalist consumption, in terms of real labor commanded, will go towards investment.
Investment = S - Capitalist Consumption
Now we have finally arrived at investment, we can see how Investment and Depreciation changes the capital stock as a whole.
Capital Stock = Capital Stock + Investment - C
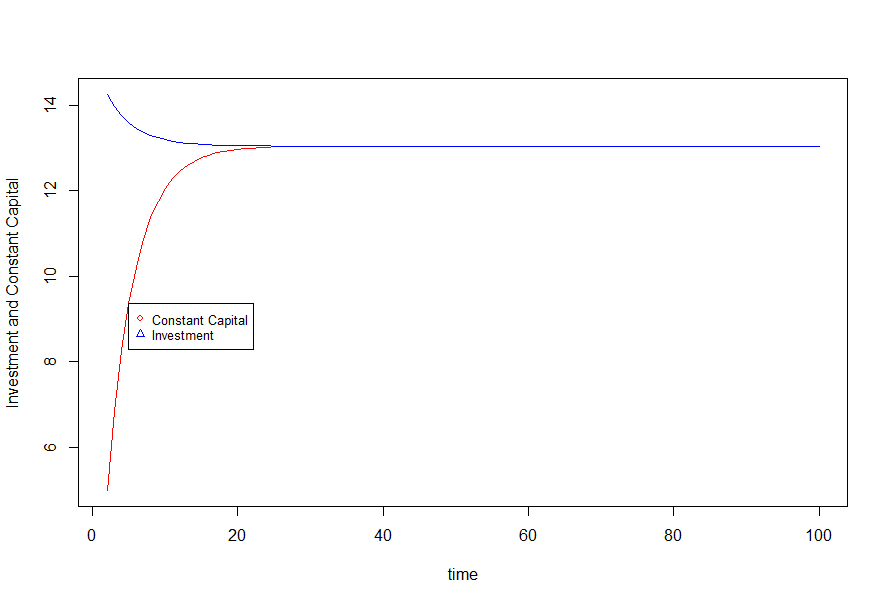
With these equations and matrices of the independent variables, we can iterate however many production cycles we like. If we like, we can hold the independent variables steady, and see what equilibrium the model reaches as the Capital Stock changes.
What this simple model shows us is that there are three things which determine the tendency for the rate of profit.
The first is the relationship between Investment and Constant Capital. These two variables will always move towards convergence. If Investment is greater than Constant Capital, you get a falling rate of profit as investment decreases, converging towards depreciation. If Investment is lesser than Constant Capital, then you will have a rising rate of profit as investment increases.

The second is the result of a changing rate of exploitation. This one is rather straightforward. A rate of exploitation of 100% means that all of labor is going towards capitalist income - however this is a physical impossibility, as it means that labor would be unable to reproduce itself. A rate of exploitation of 0% will mean that the rate of profit is necessarily 0 as well. Rising rate of exploitation will mean higher profits, all other things being equal, and vice versa. In contrast to a falling rate of profit resulting from a higher organic capital composition, falling profits from a falling rate of exploitation will tend to produce a falling organic capital composition due to lower levels of the surplus from which investment is drawn. And indeed the opposite is also true, a rising rate of exploitation is a way you achieve both a rising organic capital composition and a rising rate of profit.

The last is perhaps the most interesting. This is the effect of the rate of capitalist consumption, and by extension investment decisions by the capitalist class. Besides the initial convergence between investment and constant capital, it’s this change which is most closely related to how Marx describes the rate of profit would fall. After all, what must capitalists do when faced with competition - it is those firms, those capitalists, which invest in labor saving technology that will succeed - they must invest more and more of their income to continue their existence as capitalists.
In this model, there is a zero sum gain between investment and capitalist consumption, we are looking at the labor used to produce the consumption goods vs the investment goods as a share of the total labor. However, this model doesn’t contradict the Kalecki profit equations, except in one respect - depreciation is treated as a cost (as firms treat it) rather than a part of profits.
When investment rises as a share of surplus, the rate of profit will fall, and vice versa. In fact, if capitalist consumption falls to zero, the rate of profit will converge to the rate of exploitation. It is because of this property that changes in the level of capitalist consumption cannot overcome a secular trend in the rate of exploitation. This makes sense if we considered the two equations for the rate of profit and the (modified) rate of exploitation.
Rate of Profit : S/(C+V)
Rate of Exploitation: S/(S+V)
When investment takes up all of surplus, Constant Capital will converge with Surplus, and the two equations will be equivalent. Fortunately, because the rate of exploitation is relatively stable in history, this doesn’t cause exploitation to determine what kind of tendency the rate of profit has, merely what it’s end point will be in any given society. After all, the rate of exploitation has a maximum in the length of the working day and the necessity of reproducing labor. Some labor must be spent on making food, clothing, shelter and other consumption goods for workers.

Thus Marx’s theory of a tendency of a falling rate of profit due to rising constant capital has legs. This situation isn’t simply entailed by Marx’s account of a falling rate of profit though - it’s also entailed in his description of how capitalism would undermine its foundations, and the absolute number of capitalists shrink through competition and consolidation until industry is expropriated by the state in state capitalism - thus requiring zero labor towards capitalist consumption. In this sense, the tendency for the rate of profit to fall, and “negation of the negation” spoke of in Capital vol 1 are closely related.
Given these three mathematical forces potentially acting upon the rate of profit, it should be noted that Marx’s tendency for the rate of profit to fall is not a law of mathematical necessity, as some like Heinrich have claimed, but a historical and statistical law. But it is a form of necessity - it is not necessary to all the potential forms of capitalism, its variations and degenerations, in this sense it is historically contingent. But it is a necessary aspect to the full development of capital, in order for capital to oversee the full socialization or production and bring about the socialization of property as well. In order for capital to fully rationalize production - to employ labor-saving technology to the fullest extent and eliminate the excess of the capitalist class.
This rationalization was the way capitalism generally developed, aside from long depressions, until the end of the social democratic period and the beginning of neoliberalism, when suddenly investment ceased to increase as a share of surplus. I have written about this dynamic recently, and the role it played in stunting technological development in America and lowering average productivity growth
There are, of course, limits to this model. It is not a model for growth, though I believe that history has shown the capital accumulation and investment can help to boost productivity and growth. It does not show how increases in productivity can change the distribution of income, or other such feedback loops, as this distribution is treated as independent variables via the rate of exploitation and capitalist consumption.
The second unsaid part of this model is the natural difference between dead labor and living labor. While living labor requires contemporary physical activity, dead labor is labor from previous production cycles which has been congealed into the means of production. But not even dead labor is immortal, it can die twice as it is used up, and transfers its value into final use commodities. It is this amount which is used up which is actually expressed in Constant Capital in any given production cycle, and it is this amount which converges with investment as a share of total labor. After all, the amount invested can never exceed the total surplus in an economy, which is a part of living labor.
But because this labor is not presently being commanded, it can be wasted, if some dead labor cannot, for whatever reason, be put into the productive process. Whether because falling demand or changing techniques makes them obsolete, or because it is destroyed in war, or simply because managers and workers refuse to put it into use. These factors cannot be underestimated - the massive amount of capital destroyed in the World Wars was able to greatly boost the global rate of profit.
This destruction of capital is a fundamentally regressive force - it affords capitalist luxury at the expense of economic development. Presently, we have arrived at a stable equilibrium where Investment and Constant Capital have converged to a ratio of about 1 due to the stability of the rates of capitalist consumption and exploitation since neoliberalism began. Unless we begin to see capitalist consumption as a share of surplus begin to fall again, we will not be seeing a return to the tendency for the rate of profit to fall, and neither will we see the development of Capital into a force pushing us beyond the limits of capitalism.







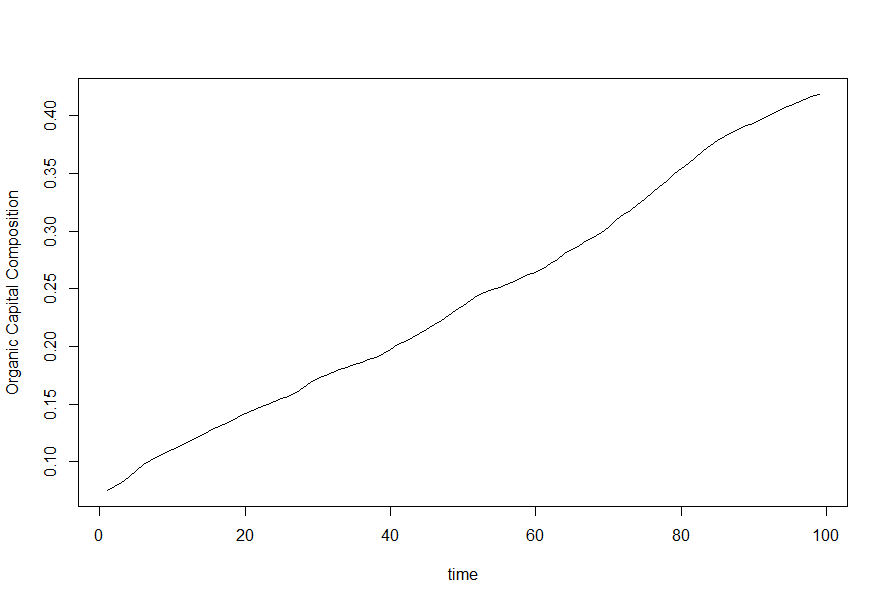


I have to challenge this last assertion.
"Unless we begin to see capitalist consumption as a share of surplus begin to fall again, we will not be seeing ... the development of Capital into a force pushing us beyond the limits of capitalism.